VSWR, დაბრუნების დანაკარგი (RL), არეკლილი სიმძლავრე და გადაცემული სიმძლავრე

ძაბვის მდგომი ტალღის თანაფარდობას (VSWR), დაბრუნების დანაკარგს (RL), არეკლილ სიმძლავრესა და გადაცემულ სიმძლავრეს შორის ურთიერთკავშირი არეკვლის კოეფიციენტის (Γ) მეშვეობით არის დაკავშირებული. ქვემოთ მოცემულია გარდაქმნის ძირითადი ფორმულები და ნაბიჯები:

### **ძირითადი ფორმულები**
1. **არეკვლის კოეფიციენტი (Γ)**:

\გამა = \frac{\text{VSWR} - 1}{\text{VSWR} + 1}

2. **VSWR** Γ-დან:

\text{VSWR} = \frac{1 + |\გამა|}{1 - |\გამა|}

3. **დაბრუნების დანაკარგი (RL)** დბ-ში:

\text{RL (დბ)} = -20 \log_{10}(|\გამა|)

4. **ასახული სიმძლავრე (%)**:

P_{\text{refl}} = |\გამა|^2 \ჯერ 100\%

5. **გადაცემული სიმძლავრე (%)**:

P_{\text{trans}} = \left(1 - |\Gamma|^2\right) \ჯერ 100\%

---

### **კონვერტაციის ნაბიჯები**
#### **1. დაწყებული VSWR-ით**:
- გამოთვალეთ Γ:

\გამა = \frac{\text{VSWR} - 1}{\text{VSWR} + 1}

- Γ გამოიყენეთ RL-ის, არეკლილი და გადაცემული სიმძლავრის საპოვნელად ზემოთ მოცემული ფორმულების გამოყენებით.

#### **2. დაბრუნების დანაკარგით დაწყება (RL დბ-ში)**:
- გამოთვალეთ Γ:

|\გამა| = 10^{-\text{RL}/20}

- გამოიყენეთ Γ VSWR-ის, არეკლილი და გადაცემული სიმძლავრის საპოვნელად.

#### **3. არეკლილი/გადაცემული სიმძლავრით დაწყება**:
- **არეკლილი სიმძლავრისთვის** (\(P_{\text{refl}}\)):

|\გამა| = \sqrt{\frac{P_{\text{refl}}}{100}}

- **გადაცემული სიმძლავრისთვის** (\(P_{\text{ტრანს}}\)):

|\გამა| = \sqrt{1 - \frac{P_{\text{ტრანს}}}{100}}

- გამოიყენეთ Γ VSWR-ის და RL-ის გამოსათვლელად.

---

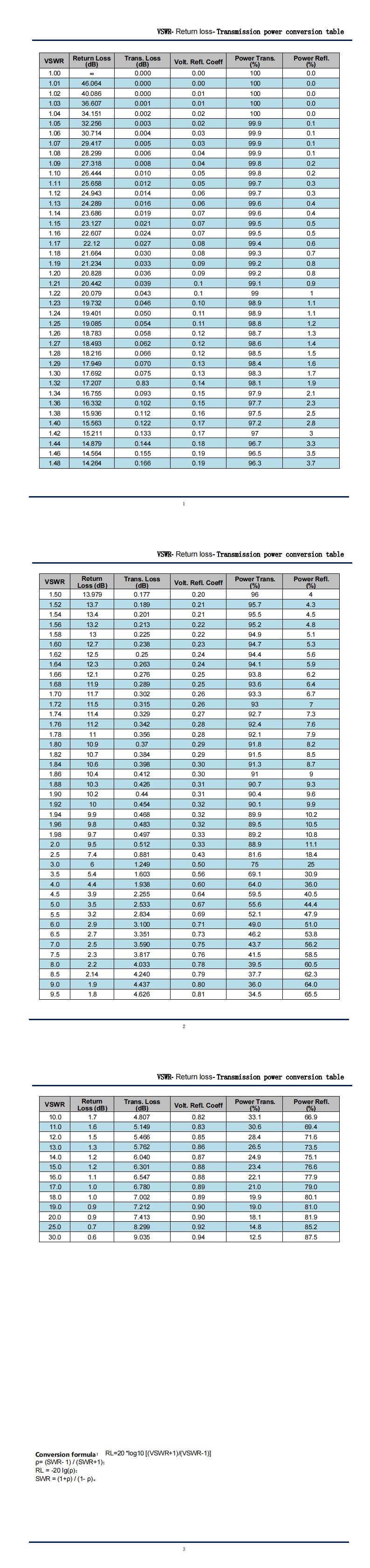
### **ცხრილის მაგალითი**
| **VSWR** | **დაბრუნების დანაკარგი (dB)** | **არეკლილი სიმძლავრე (%)** | **გადაცემული სიმძლავრე (%)** |
|----------|------------------------|--------------------------|---------------------------------|
| 1.0 | ∞ (იდეალური შესაბამისობა) | 0% | 100% |
| 1.5 | 14.0 დბ | 4% | 96% |
| 2.0 | 9.5 დბ | 11.1% | 88.9% |
| 3.0 | 6.0 დეციბელი | 25% | 75% |

---

### **ძირითადი შენიშვნები**
- **1:1** VSWR არეკვლის არარსებობას ნიშნავს (Γ = 0, RL = ∞).
- **უფრო მაღალი VSWR** ან **დაბალი RL** მიუთითებს არეკლილი სიმძლავრის ზრდაზე.
- **გადაცემული სიმძლავრე** მაქსიმალურად გამოიყენება, როდესაც VSWR ≈ 1-ის ტოლია.

გამოიყენეთ ეს ფორმულები რადიოსიხშირულ სისტემებში წინაღობის შესაბამისობის პარამეტრების ურთიერთგარდასაქმებლად.